Introduction To LLMs Text Embeddings For SEO With Examples

In case you are an web optimization practitioner or digital marketer studying this text, you might have experimented with AI and chatbots in your on a regular basis work.

However the query is, how are you going to take advantage of out of AI apart from utilizing a chatbot person interface?

For that, you want a profound understanding of how giant language fashions (LLMs) work and study the fundamental stage of coding. And sure, coding is totally essential to succeed as an web optimization skilled these days.

That is the primary of a collection of articles that intention to stage up your expertise so you can begin utilizing LLMs to scale your web optimization duties. We imagine that sooner or later, this ability can be required for fulfillment.

We have to begin from the fundamentals. It should embrace important info, so later on this collection, it is possible for you to to make use of LLMs to scale your web optimization or advertising efforts for probably the most tedious duties.

Opposite to different related articles you’ve learn, we’ll begin right here from the top. The video beneath illustrates what it is possible for you to to do after studying all of the articles within the collection on how one can use LLMs for web optimization.

Our group makes use of this software to make inner linking quicker whereas sustaining human oversight.

Did you prefer it? That is what it is possible for you to to construct your self very quickly.

Now, let’s begin with the fundamentals and equip you with the required background data in LLMs.

What Are Vectors?

In arithmetic, vectors are objects described by an ordered checklist of numbers (elements) equivalent to the coordinates within the vector area.

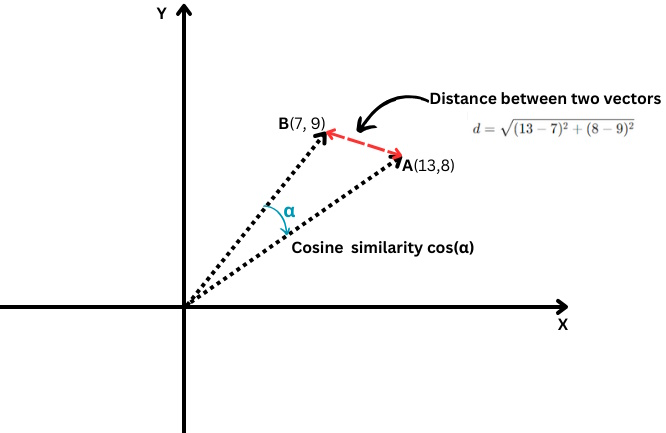
A easy instance of a vector is a vector in two-dimensional area, which is represented by (x,y) coordinates as illustrated beneath.

On this case, the coordinate x=13 represents the size of the vector’s projection on the X-axis, and y=8 represents the size of the vector’s projection on the Y-axis.

Vectors which can be outlined with coordinates have a size, which is named the magnitude of a vector or norm. For our two-dimensional simplified case, it’s calculated by the formulation:

$L=\sqrt{({}_{}{x}_1{)}^2+(y_1{)}^2}$

Nonetheless, mathematicians went forward and outlined vectors with an arbitrary variety of summary coordinates (X1, X2, X3 … Xn), which is named an “N-dimensional” vector.

Within the case of a vector in three-dimensional area, that might be three numbers (x,y,z), which we will nonetheless interpret and perceive, however something above that’s out of our creativeness, and every little thing turns into an summary idea.

And right here is the place LLM embeddings come into play.

What Is Textual content Embedding?

Textual content embeddings are a subset of LLM embeddings, that are summary high-dimensional vectors representing textual content that seize semantic contexts and relationships between phrases.

In LLM jargon, “phrases” are known as knowledge tokens, with every phrase being a token. Extra abstractly, embeddings are numerical representations of these tokens, encoding relationships between any knowledge tokens (items of knowledge), the place an information token will be a picture, sound recording, textual content, or video body.

To be able to calculate how shut phrases are semantically, we have to convert them into numbers. Identical to you subtract numbers (e.g., 10-6=4) and you may inform that the gap between 10 and 6 is 4 factors, it’s attainable to subtract vectors and calculate how shut the 2 vectors are.

Thus, understanding vector distances is vital as a way to grasp how LLMs work.

There are alternative ways to measure how shut vectors are:

1. Euclidean distance.
2. Cosine similarity or distance.
3. Jaccard similarity.
4. Manhattan distance.

Every has its personal use instances, however we’ll focus on solely generally used cosine and Euclidean distances.

What Is The Cosine Similarity?

It measures the cosine of the angle between two vectors, i.e., how carefully these two vectors are aligned with one another.

Euclidean distance vs. cosine similarity

It’s outlined as follows:

$$\cos \left(\alpha \right)=\frac{A\cdot B}{\mid A\mid \cdot \mid B\mid }$$

The place the dot product of two vectors is split by the product of their magnitudes, a.ok.a. lengths.

Its values vary from -1, which implies utterly reverse, to 1, which implies equivalent. A worth of ‘0’ means the vectors are perpendicular.

By way of textual content embeddings, reaching the precise cosine similarity worth of -1 is unlikely, however listed here are examples of texts with 0 or 1 cosine similarities.

Cosine Similarity = 1 (Equivalent)

1. “High 10 Hidden Gems for Solo Vacationers in San Francisco”
2. “High 10 Hidden Gems for Solo Vacationers in San Francisco”

​These texts are equivalent, so their embeddings can be the identical, leading to a cosine similarity of 1.

Cosine Similarity = 0 (Perpendicular, Which Means Unrelated)

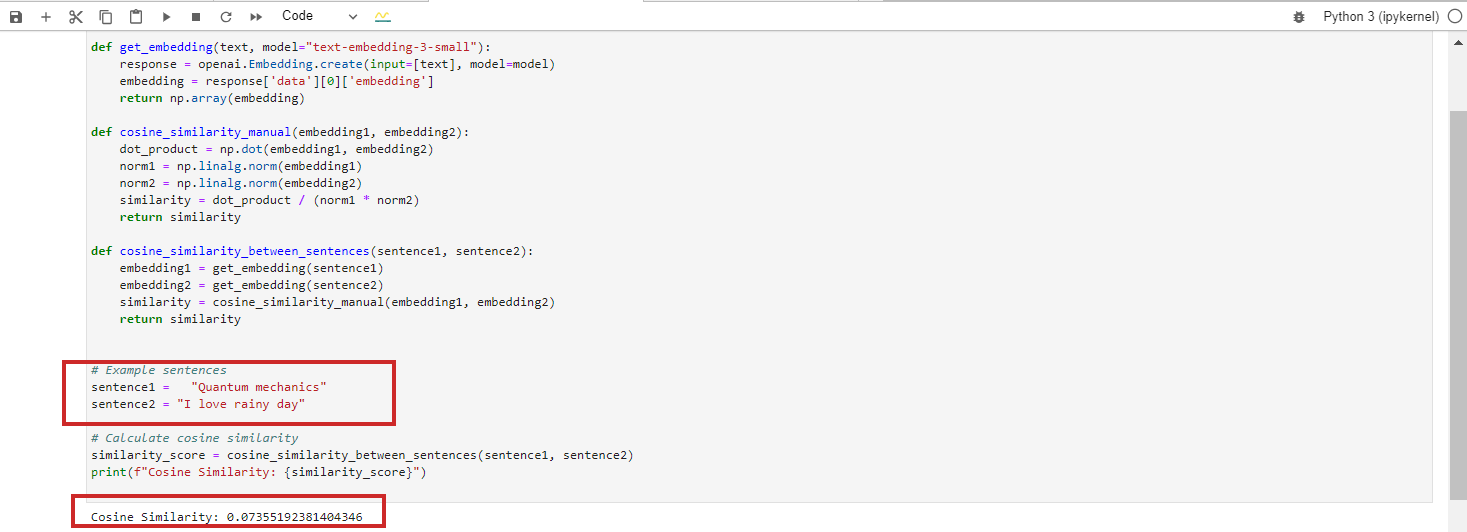
1. “Quantum mechanics”
2. “I like wet day”

​These texts are completely unrelated, leading to a cosine similarity of 0 between their BERT embeddings.

Nonetheless, for those who run Google Vertex AI’s embedding mannequin ‘text-embedding-preview-0409’, you’re going to get 0.3. With OpenAi’s ‘text-embedding-3-large’ fashions, you’re going to get 0.017.

(Observe: We’ll study within the subsequent chapters intimately working towards with embeddings utilizing Python and Jupyter).

We’re skipping the case with cosine similarity = -1 as a result of it’s extremely unlikely to occur.

When you attempt to get cosine similarity for textual content with reverse meanings like “love” vs. “hate” or “the profitable venture” vs. “the failing venture,” you’re going to get 0.5-0.6 cosine similarity with Google Vertex AI’s ‘text-embedding-preview-0409’ mannequin.

It’s as a result of the phrases “love” and “hate” typically seem in related contexts associated to feelings, and “profitable” and “failing” are each associated to venture outcomes. The contexts during which they’re used may overlap considerably within the coaching knowledge.

Cosine similarity can be utilized for the next web optimization duties:

1. Classification.
2. Key phrase clustering.
3. Implementing redirects.
4. Inside linking.
5. Duplicate content material detection.
6. Content material advice.
7. Competitor evaluation.

Cosine similarity focuses on the course of the vectors (the angle between them) reasonably than their magnitude (size). In consequence, it will probably seize semantic similarity and decide how carefully two items of content material align, even when one is for much longer or makes use of extra phrases than the opposite.

Deep diving and exploring every of those can be a objective of upcoming articles we’ll publish.

What Is The Euclidean Distance?

In case you might have two vectors A(X1,Y1) and B(X2,Y2), the Euclidean distance is calculated by the next formulation:

$D=\sqrt{(x_2-x_1{)}^2+(y_2-y_1{)}^2}$

It’s like utilizing a ruler to measure the gap between two factors (the crimson line within the chart above).

Euclidean distance can be utilized for the next web optimization duties:

1. Evaluating key phrase density within the content material.
2. Discovering duplicate content material with an identical construction.
3. Analyzing anchor textual content distribution.
4. Key phrase clustering.

Right here is an instance of Euclidean distance calculation with a worth of 0.08, almost near 0, for duplicate content material the place paragraphs are simply swapped – which means the gap is 0, i.e., the content material we examine is identical.

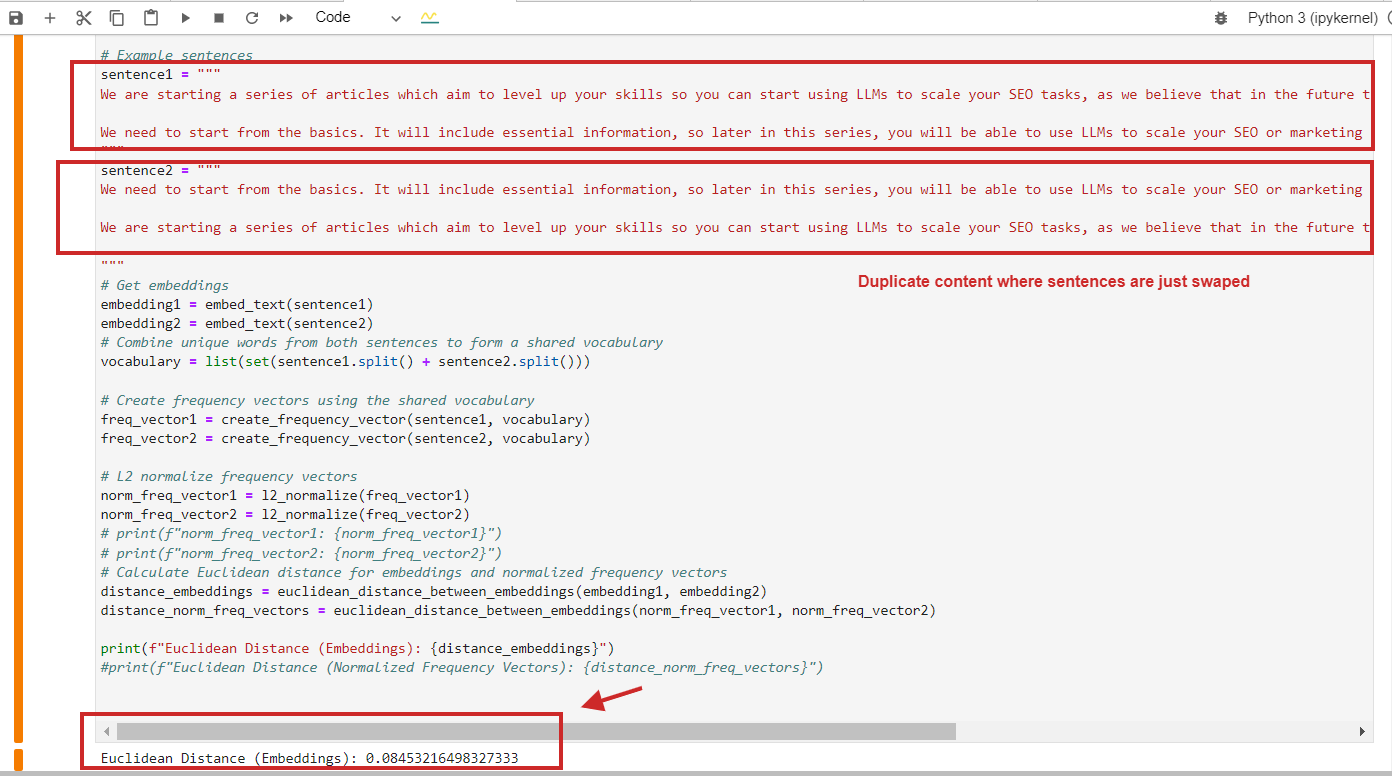Euclidean distance calculation instance of duplicate content material

In fact, you should use cosine similarity, and it’ll detect duplicate content material with cosine similarity 0.9 out of 1 (nearly equivalent).

Here’s a key level to recollect: You shouldn’t merely depend on cosine similarity however use different strategies, too, as Netflix’s analysis paper means that utilizing cosine similarity can result in meaningless “similarities.”

We present that cosine similarity of the realized embeddings can the truth is yield arbitrary outcomes. We discover that the underlying cause just isn’t cosine similarity itself, however the truth that the realized embeddings have a level of freedom that may render arbitrary cosine-similarities.

As an web optimization skilled, you don’t want to have the ability to absolutely comprehend that paper, however do not forget that analysis exhibits that different distance strategies, such because the Euclidean, ought to be thought-about based mostly on the venture wants and end result you get to scale back false-positive outcomes.

What Is L2 Normalization?

L2 normalization is a mathematical transformation utilized to vectors to make them unit vectors with a size of 1.

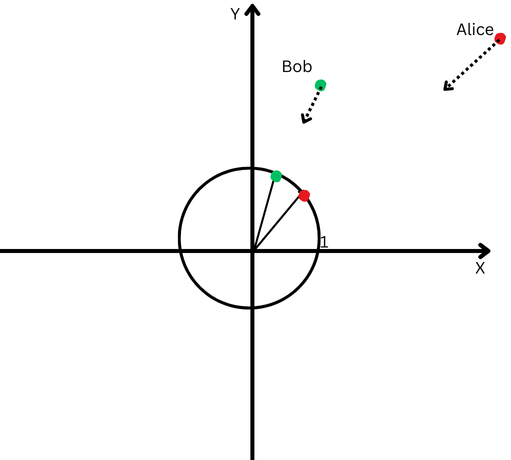
To clarify in easy phrases, let’s say Bob and Alice walked an extended distance. Now, we need to examine their instructions. Did they observe related paths, or did they go in utterly completely different instructions?

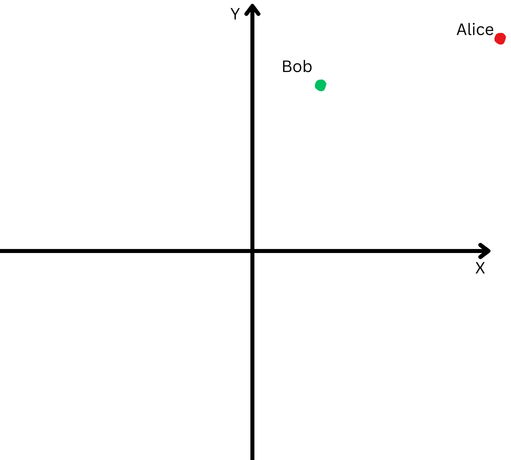“Alice” is represented by a crimson dot within the higher proper quadrant, and “Bob” is represented by a inexperienced dot.

Nonetheless, since they’re removed from their origin, we could have problem measuring the angle between their paths as a result of they’ve gone too far.

However, we will’t declare that if they’re removed from one another, it means their paths are completely different.

L2 normalization is like bringing each Alice and Bob again to the identical nearer distance from the start line, say one foot from the origin, to make it simpler to measure the angle between their paths.

Now, we see that regardless that they’re far aside, their path instructions are fairly shut.

A Cartesian aircraft with a circle centered on the origin.

Which means we’ve eliminated the impact of their completely different path lengths (a.ok.a. vectors magnitude) and may focus purely on the course of their actions.

Within the context of textual content embeddings, this normalization helps us deal with the semantic similarity between texts (the course of the vectors).

Many of the embedding fashions, akin to OpeanAI’s ‘text-embedding-3-large’ or Google Vertex AI’s ‘text-embedding-preview-0409’ fashions, return pre-normalized embeddings, which implies you don’t must normalize.

However, for instance, BERT mannequin ‘bert-base-uncased’ embeddings are usually not pre-normalized.

Conclusion

This was the introductory chapter of our collection of articles to familiarize you with the jargon of LLMs, which I hope made the knowledge accessible without having a PhD in arithmetic.

When you nonetheless have bother memorizing these, don’t fear. As we cowl the subsequent sections, we’ll seek advice from the definitions outlined right here, and it is possible for you to to know them via observe.

The subsequent chapters can be much more fascinating:

• Introduction To OpenAI’s Textual content Embeddings With Examples.
• Introduction To Google’s Vertex AI Textual content Embeddings With Examples.
• Introduction To Vector Databases.
• How To Use LLM Embeddings For Inside Linking.
• How To Use LLM Embeddings For Implementing Redirects At Scale.
• Placing It All Collectively: LLMs-Primarily based WordPress Plugin For Inside Linking.

The objective is to stage up your expertise and put together you to face challenges in web optimization.

Lots of you could say that there are instruments you should purchase that do most of these issues mechanically, however these instruments won’t be able to carry out many particular duties based mostly in your venture wants, which require a customized method.

Utilizing web optimization instruments is at all times nice, however having expertise is even higher!

Extra assets:

Featured Picture: Krot_Studio/Shutterstock